manjaro
123错误:manjaro-keyring: 来自 "*** <***@manjaro.org>" 的签名是未知信任的:: 文件 /var/cache/pacman/pkg/manjaro-keyring-20220514-2-any.pkg.tar.zst 已损坏 (无效或已损坏的软件包 (PGP 签名)).打算删除吗? [Y/n] y错误:无法提交处理 (无效或已损坏的软件包 (PGP 签名))
123sudo pacman-key --refresh-keyssudo pacman-key --initsudo pacman-key --populate
deepin-wine-wechat
https://blog.csdn.net/weixin_51151193/article/details/122219303
faceswap
安装
faceswap要求python 3.7/3.8而我的manjaro自带3.10。不知道为什么即便改了zsh,pyenv也没法正常工作。最后发现原来有安装脚本,会自动安装好miniconda。
[自动安装程序]([Releases · deepfakes/faceswap · GitHub]https://github.com/deepfakes/faceswap/releases(https://github.com/deepfakes/faceswap/releases))
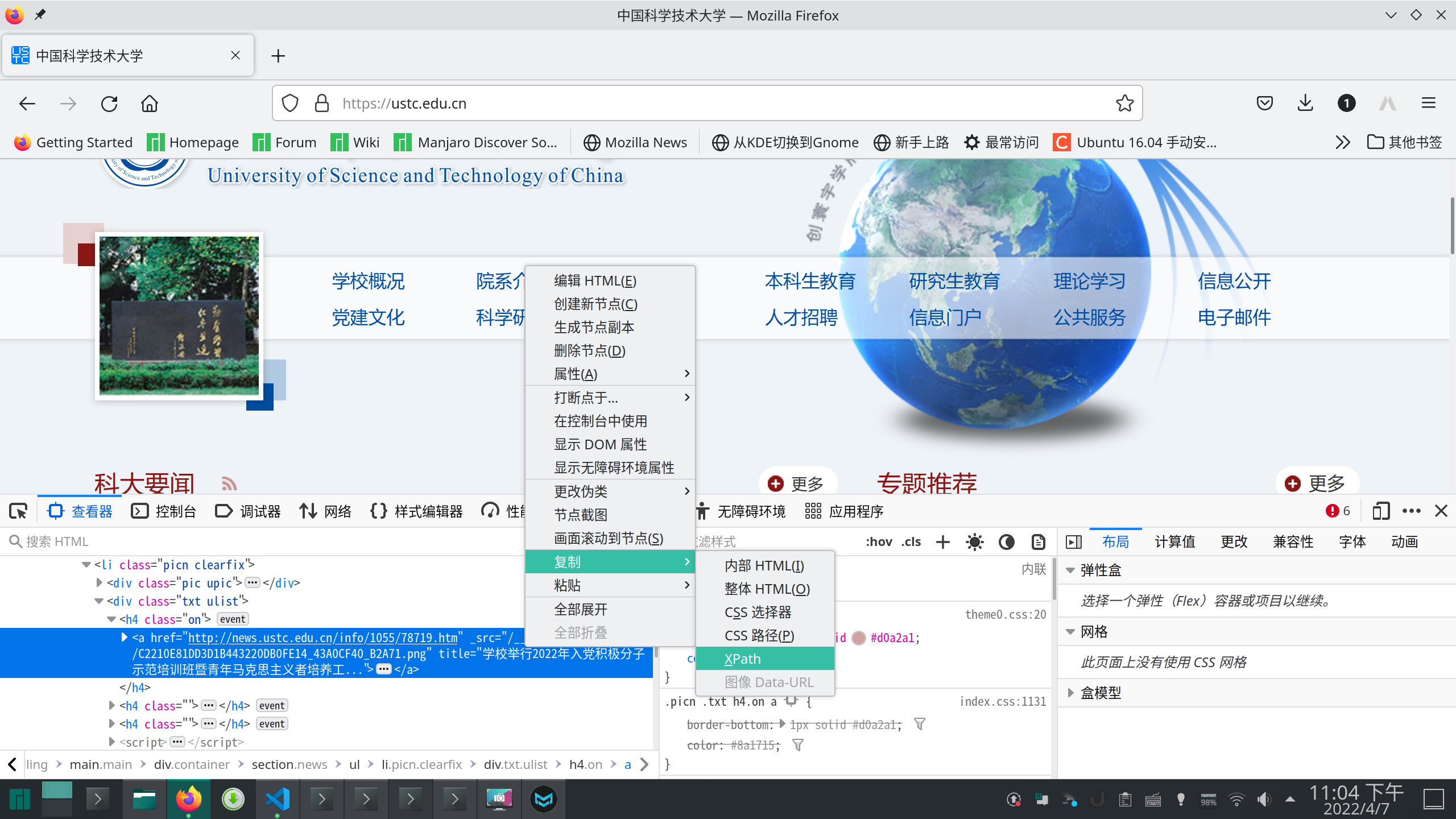
selenium
python 爬虫 基于Selenium
1.安装Selenium
pip install Selenium
2.安装浏览器驱动
用包管理器或手动安装:
Selenium3调用浏览器需要webdriver驱动
Chrome驱动文件
Firefox驱动文件
Edge驱动文件
放置到python安装目录Script下(pip --version)
参考1
参考2
AB的伴随矩阵等于B的伴随矩阵乘A的伴随矩阵
(AB)*=B*A*
一些争论
文中试图证伪流行的证法,但我认为证伪的过程并不严谨,原解答是正确的。
一些看法
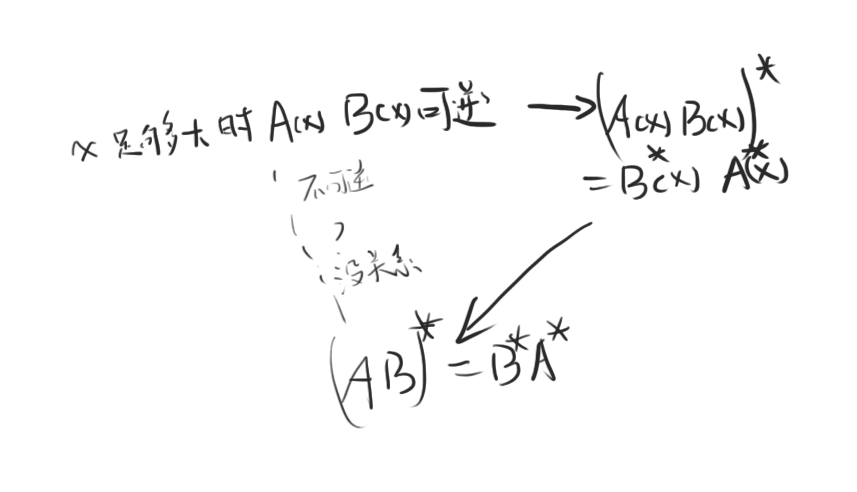
文中认为当两个矩阵A,B变成不确定的函数形式,即A(x),B(x)时 $ (A(x)B(x))∗=B(x)∗A(x)^∗ $ 是不成立的,但并没有给出充足的证据。
那我复述一遍证明的表述。令T(x)=(A(x)B(x))∗,P(x)=B(x)∗A(x)∗T(x)=(A(x)B(x))^∗,P(x)=B(x)^∗A(x)^∗T(x)=(A(x)B(x))∗,P(x)=B(x)∗A(x)∗ ,显然 $$ T(x){ij},P(x){ij} $$
是都是关于x的多项式,且都是确定的(可以用任何一种展开方式算出来)。令f(x)=P(x)ij−Q(x)ijf(x)=P(x)_{ij}-Q(x)_{ij}f(x)=P(x)ij−Q(x)ij,因此f(x)f(x)f(x)是关于x的多项式,而我们知道f(x)f(x)f(x)有无穷多个零点,容易得到f(x)=0f(x)=0f(x)=0 。所以f(0)=0,P(0)ij=Q(0)ijf(0)=0, ...
e380
逮捕神奇的 E380
一天,我手动编辑了我的铃声系统的database,然后:
Why? 哪儿出了问题?
我一段一段把数据重新加入数据表。终于逮到了它e380
猜猜他是什么?它是“ ”没错他就是空格。可百度上并没它e380的身影。
想到我们信息课上的诡异的感叹号,我灵机一动:是全角字符!
打开全角字符,输入空格。没错,是它。
后记
然后我的hexo炸了
以为好久不用它,什么部件升级了产生冲突,可重装也搞不定,可把我给急坏了。新年将至于是我放弃了。
时隔19天,ncov的爆发到疫情的胜利在逐渐浮现,我深知重返校园已经已经不远了。我怀着喜悦的心情,再次拿出耐心查错大法,一篇篇把文章放入。然后我开心地发现这篇文章把它搞死了
原来是它所属的文件夹里还有文件夹和一些奇奇怪怪的东西而且图片的名字也拼错了。真是太粗心了◠◡◠。
ad
做个广告http://www.jwbl.com/e/tool/gfen/?id=4919
http://www.jwbl.com/e/tool/gfen/?id=1263
http://aigei.com/?m=a_4106361
顺便统计访问人数。
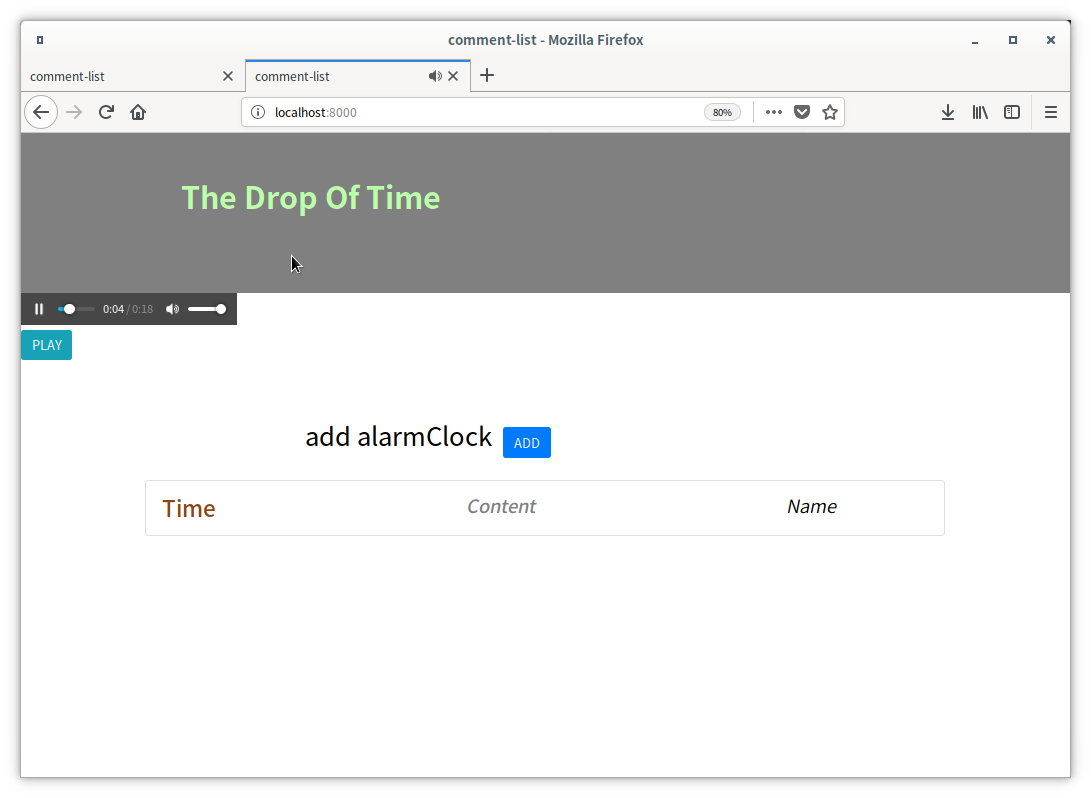
DropClock
初试nodejs,写了个闹钟。
https://github.com/FreedomXingyuLu/dropClock
数论心得
!!!参考《ACM国际大学生程序设计竞赛算法与实现》
求n!中含有某个因子个数的方法
转载自https://www.cnblogs.com/dolphin0520/archive/2011/04/11/2012891.html
12345678910int count(int n,int k){ int num=0; while(n) { num+=n/k; n/=k; } return num;}
求一个阶乘中含有的素因子2的个数
n!共
n+n2+n22+⋅⋅⋅+n2k(整除)n+ \frac{n}{2}+\frac{n}{2^2}+···+\frac{n}{2^k}(整除)
n+2n+22n+⋅⋅⋅+2kn(整除)
个二
即把它分解成二进制位,如(10100)2(10100)_2(10100)2 ,因数2的个数为 (1010)2+(101)2+(10)2+(1)2(1010)_2+(101)_2+(10)_2+(1)_2(1010)2+(101)2+(10)2+( ...