paperphotoruler
纸拍尺
今天看到别人家产品拍照时下面垫的网格纸心动了,但是在网上搜了搜却发现这个东西很小众,没找到现成现的,有的卖的说要定制,有的配色不好看,遂决定自己做一个。
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586# -*- coding: utf-8 -*-from PIL import Imagefrom PIL import ImageDrawfrom PIL import Image, ImageDraw, ImageFontimport osoutputfile="ruler.pdf"#72像素/英寸 72像素=2.54cm dpi_scale=5# 1:A4 at 72dpiprint_scale=25.0/22.7weight=595*dpi_scaleheight=842 ...
docker
tinyBipedal 计划改用 gazebo 来跑仿真,还得搞一个 Ubuntu 的 ROS 环境,但是电脑已经装不下了,悲,那就跑个能用显卡的 docker 吧。
https://docs.nvidia.com/datacenter/cloud-native/container-toolkit/latest/install-guide.html
https://blog.csdn.net/mightbxg/article/details/119733088
1234sed -i 's@//.*archive.ubuntu.com@//mirrors.ustc.edu.cn@g' /etc/apt/sources.listapt updateapt install xarclock
sudo docker run -it -p 6901:6901 -e VNC_PW=password --runtime=nvidia --gpus all --name ubuntu-desktop kasmweb/desktop:1.10.0-rolling
CRC
CRC(Cyclic Redundancy Check) 循环冗余校核,是一种根据网络数据包或电脑文件等数据产生简短固定位数校核码的快速算法。
一个简单的原理介绍视频:
https://www.youtube.com/watch?v=izG7qT0EpBw
一些代码实现
https://blog.csdn.net/liyuanbhu/article/details/7882789
在线网址:
http://www.ip33.com/crc.html
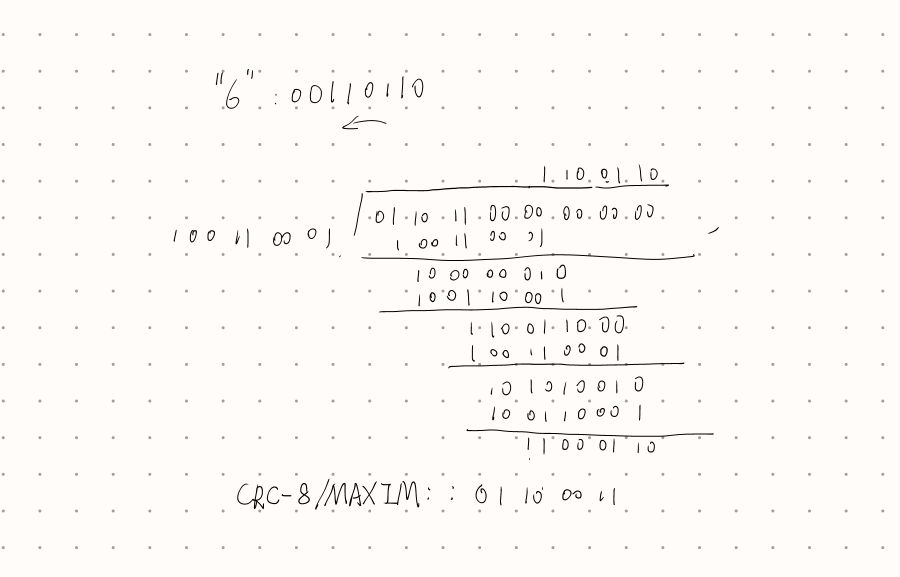
CRC 校验在布尔域上对数据做除法,得到 “checksum” ,附在数据末尾,使得数据可以在布尔意义下被除数整除即可,不同的除数具有不同的校验效果。
SummerScienceCamp
高校科学营
2023 年 7 月 18 日,中科大机器人俱乐部与 RoboWalker 战队承办了高校科学营的夜晚活动,为来自高中参加活动的同学们带来了科里科气小风扇的制作,活动取得了圆满的成功。
小风扇搭载 ESPCam ,使用 Arduino 调用 EspWho 解决方案实现人脸位置检测,并使用 PWM 驱动舵机和电机,实现小风扇追随人脸转动和吹风的效果。
前期筹划
6 月 25 日,我们在得知这个活动后报名负责组织这个活动,共五位俱乐部成员。此时正处于考试周,从龙队那里接单后暂且搁置。
7 月 1 日至 7 月 6 日,跟据之前了解的信息————带领高中的大“小朋友”们一起图形化编程————进行准备,因为去年资料丢失(?听去年负责的同学说程序是买来就烧在开发板上),只能尝试自己解决。
就软件上满足需求有两个重点,一是人脸的识别,二是图形化编程。在人脸识别上有两种方案,要么让 ESPCam 推流,交给服务器跑神经网络识别人脸,再返回数据给开发板(觉得 Cam 性能不足),二是直接在板子上跑网络或者有库可以调用。第一个方法虽然可靠,一旦离开了服务器也就是大家把作品带回家,这个小风 ...
CollisionSoundDetection
碰撞声音检测
留一个坑
通过检测声音的特征来识别打击是否命中装甲板,进而实现命中率检测的效果。
哈人检测器
哈人检测器
用于 LUG 西区图书馆 206 活动室是否有人的检测。
网页 206.rtxux.xyz
硬件
esp32-nico
机器人社团地上随手捡的红外传感器
软件
Arduino Github
Rust开发的服务端(by rtxux) 206.rtxux.xyz
Balance-bot
Robowalker 平衡步兵参与开发寄录
2023/2/8
轮子的电机有一个体质不行,用手就能把它掰到堵转,再买一个吧。
AK10-9电机,店家上位机的设计有点抽象,研究了好久,不会,联系客服。
2023/2/9
在客服的指导下,AK10-9电机成功控制运动,昨天的问题是我们的驱动板没有伺服模式,但我们一直企图打开它。
晚:3个连在一条can线上的电机的can被一波带走,原因未知。
2022/2/14
仿真持续改进,尝试S型速度曲线控制,却产生超大前摇和刹车不灵。
2022/2/15
电机换了新的增强了的驱动版和四块旧驱动版回来了。3200,死鬼死贵的。
2022/2/16
开始移植仿真环境到平衡车上,但是没有成功。开始是单片机程序挂了。先怀疑算不过来,但又不太可能。开大系统栈和堆,无效。发现printf多发会吧程序卡死。发现吸臭氧能让程序活过来。最后, ddd张昊鹏发现是freertos的给进程的空间开小了。
2022/2/17
平衡车动了,但是会抖。要考试,停工。
2022/3/5
尝试用pid先站起来,发现轮毂电机也出锅。
不同前缀的脉塔智能是不同的店,买了 ...
PPKA
2022RoboGame 壶壶绝杀队技术总结
写在前面
这里是壶壶绝杀队(AKA.PPKA)2022RoboGmae技术总结。
参赛项目:冰壶机器人
参赛队员介绍:林文浩 刘思源 张昊鹏 卢星宇 蒋宇航
OverView
机械
为了适应本次比赛任务的特殊性,我们队在机械结构上进行了很大的创新,我们将移动型龙门架和移动底盘有机地结合在一起,使得我们的机器人能够在不转身的情况下对前方和后方的冰壶都能进行拾取,大大提高了机器人抓取冰壶的灵活性。其实也没快很多但是很炫。
同时,我们队率先性地开创了采用气动装置发射冰壶的方法,这种方式在比赛中被证明是十分稳定的,而且大大降低了制作成本。除了在大体结构上进行有效创新,我们还在各项细节处不断打磨,追求让机器人达到最好的效果,比如我们特意让真空泵理吸盘尽量距离近,保证气路上漏气的现象明显减少,而且为了防止单个真空泵故障导致失误,我们还设计了双真空泵的结构,这样子即使一个真空泵发生故障而不工作,机器人依然可以完成各项任务。再比如我们还在车上挂有额外的电磁阀,当一个电磁阀坏掉的时候依然可以迅速替换备用电磁阀继续工作。
车身总体的设计过程中,我们 ...
blogSetUp
使用hexo和butterfly主题。
image.pngimage.png
一些butterfly配置
https://zhuanlan.zhihu.com/p/492207978
一些美化
https://www.cnblogs.com/MoYu-zc/p/14395965.html
git hook 和nginx
latex 解决一些渲染冲突
https://www.jianshu.com/p/9b9c241146bc
通过Github pages将自己的域名解析至博客园或其他网站 - 梅雨明夏 - 博客园
servermail
当服务器有人ssh登陆root的时候发邮件通知,守护服务器安全
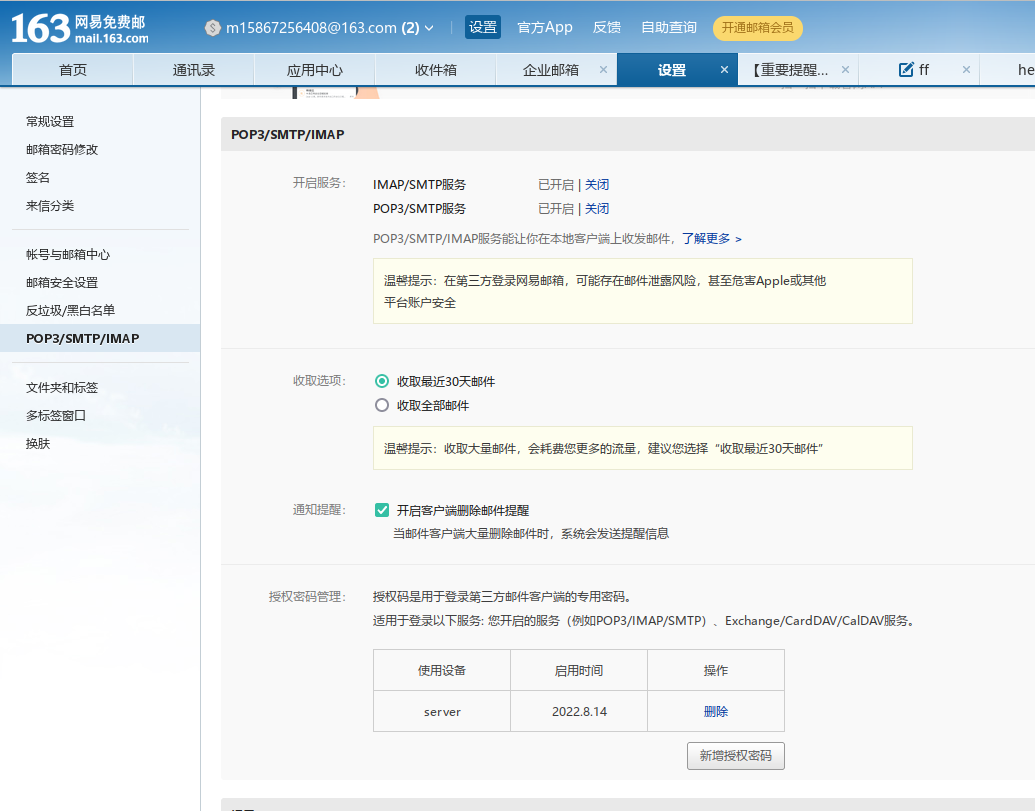
注册并配置邮箱
记得记录密码
设置发信邮箱
修改/etc/mail.rc,在文件末尾增加以下内容,指定外部的smtp服务器地址、帐号密码等$ vi /etc/mail.rc
12345set [email protected] smtp=smtp.163.com set [email protected] smtp-auth-password=刚才的密码set smtp-auth=login
命令来发送邮件
1echo hello word | mail -s " title" [email protected]
设置登陆时通知
1echo -e "ALERT - SSH root shell access \n Device: "$HOSTNAME" \n Time:" `date`"\n User:" `who` | mail -s "Alert: SSH r ...