(AB)*=B*A*

一些争论

1.png

文中试图证伪流行的证法，但我认为证伪的过程并不严谨，原解答是正确的。

一些看法

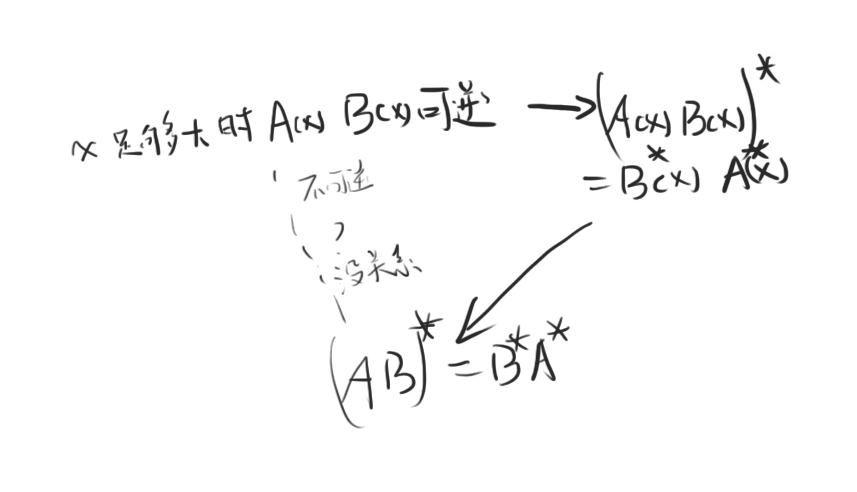
​ 文中认为当两个矩阵A，B变成不确定的函数形式，即A(x),B(x)时 $ (A(x)B(x))∗=B(x)∗A(x)^∗ $ 是不成立的,但并没有给出充足的证据。

​ 那我复述一遍证明的表述。令T(x)=(A(x)B(x))∗,P(x)=B(x)∗A(x)∗T(x)=(A(x)B(x))^∗,P(x)=B(x)^∗A(x)^∗ ，显然 $$ T(x){ij},P(x){ij} $$
是都是关于x的多项式，且都是确定的(可以用任何一种展开方式算出来)。令f(x)=P(x)ij−Q(x)ijf(x)=P(x)_{ij}-Q(x)_{ij},因此f(x)f(x)是关于x的多项式，而我们知道f(x)f(x)有无穷多个零点，容易得到f(x)=0f(x)=0 。所以f(0)=0,P(0)ij=Q(0)ijf(0)=0,P(0)_{ij}=Q(0)_{ij} 而由i,ji,j的任意性， $P(0)=Q(0)，(A(0)B(0))∗=B(0)∗A(0)∗，(AB)∗=B∗A∗ $

​ 逻辑流畅通顺并未出现漏洞。再看一眼文中如何证伪：“若x=0，则A(x)也为不可逆状态也就不符合A和B均为方阵的条件”，这句话是自相矛盾，而且我们要证明的就是A(0)B(0)不可逆时成立呀，AB不可逆怎么又成为证伪的证据？

​ 我认为证伪不成立，原证法正确。

​ 再补充一下为什么A(x)当x足够大时能够可逆。回想起助教讲的巧妙证法：|A(x)|是关于x的n次多项式，则必有小于等于n个的实数根，当x大于最大的根a0a0时，|A(x)|就不等于零，就可逆了。同理也存在实数a1a1，使得当x>a1a1时使|B(x)|也不为零。那么当x≥max{a0,a1}x\ge max\{a0,a1\}时，A(x),B(x),A(x)B(x)都可逆了。

一些故事

​ 当初在证这个式子时上网搜索，搜到了流行证法，不过看不太懂有点迷惑，然后有看到了这篇杂志，我点点头，心想：是的，我看不懂的证明肯定是错的。然而文中的朴素做法有点吓人，收藏再见。

​ 第二次见它是在习题课上，助教津津有味的讲解，而我怀着看过这篇文章的傲慢，对旁边的人说你上网搜搜看，助教的证法是错的。结果在聊天的过程中助教把题讲完了，没听懂。

​ 再次，看卡莱-哈密顿定理时似乎打通了筋脉，忽然联想到了它，原来流行证法是这个意思，兴致大发写下此文，然后发现卡莱-哈密顿定理的证明又看不懂了。
2.png